Cosine similarity measures the angle between two non-zero vectors of an inner product space. In Python, the cosine similarity is calculated by taking the “dot” product of the vector and dividing it by the magnitude product of the vector. Python provides different modules, such as “scikit-learn”, “scipy”, etc., for calculating the cosine similarity of 1-D or 2-D vectors.
Various methods are used to calculate the cosine similarity in Python. Here are the methods for calculating cosine similarity:
Method 1: Using Numpy Module
The Numpy module provides a function “np.array()”, “np.dot()” and “norm()” to calculate the cosine similarity in Python. Let’s understand it by the following examples:
Example 1: Finding the Cosine Similarity of Two 1-D Vectors
In the below code, the cosine similarity between two “1-D” vectors is calculated using different functions of the Numpy module:
Code:
import numpy
from numpy.linalg import norm
v1 = numpy.array([2,1,2,3,2,9])
v2 = numpy.array([3,4,2,4,5,5])
print(numpy.dot(v1,v2)/(norm(v1)*norm(v2)))
In the above code:
- The “np.array()” function is used to create the “1-D” vector by accepting the element of the list as an argument.
- The “np.dot()” function accepts the vector “v1” and vector “v2” as an argument and returns the dot product.
- The “norm()” function accepts the vector as an argument and returns the vector norm.
- The dot product of two given vectors is divided by the multiplication of two vector norms to get the cosine similarity in Python.
Output:

The above output shows the cosine similarity of the input “1-D” vectors.
Example 2: Finding the Cosine Similarity of Two 2-D Vectors
In the below code, the cosine similarity between two “2-D” vectors is calculated using the Numpy module:
Code:
import numpy
from numpy.linalg import norm
v1 = numpy.array([[1,2,3],[3,2,1],[-2,1,-3]])
v2 = numpy.array([[4,2,4],[2,-2,5],[3,4,-4]])
print(numpy.sum(v1*v2, axis=1)/(norm(v1, axis=1)*norm(v2, axis=1)))
In the above code:
- The “np.array()” function is used to create the “2-D” arrays vector.
- The “np.sum()” function is used to add the element of the multiplicative array “v1” and “v2”.
- Next, the returned value of the “np.sum()” function is divided by the norm vector product. This calculation will return the cosine similarity of the input vector in Python.
Output:

The above output shows the cosine similarity of the input “2-D” vectors.
Method 2: Using scikit-learn Module
The “scikit-learn” module provides the function “cosine_similarity()” to calculate the cosine similarity of the input vectors:
Code:
from sklearn.metrics.pairwise import cosine_similarity,cosine_distances
import numpy
v1 = numpy.array([22,34,56,78,97])
v2 = numpy.array([32,25,35,56,77])
print(cosine_similarity(v1.reshape(1,-1),v2.reshape(1,-1)))
In the above code:
- The “np.array()” function is used to create the vectors.
- The “cosine_similarity()” function is used to calculate the cosine similarity of input vectors “v1” and “v2”.
Output:
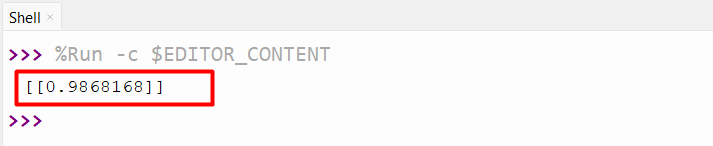
The above output shows the “cosine similarity” of two “1-D” vectors.
Method 3: Using scipy Module
The scipy module also provides a function “spatial.distance.cosine()” that is used for calculating the cosine similarity in Python:
Code:
import numpy
from scipy import spatial
v1 = numpy.array([22,34,56,78,97])
v2 = numpy.array([32,25,35,56,77])
cosim = spatial.distance.cosine(v1, v2)
print(1 - cosim)
In the above code:
- The “spatial.distance.cosine()” function is used to calculate the cosine similarity by taking the vector as an argument.
- The final calculation returned by “spatial.distance.cosine()” is subtracted from “1”.
Output:

The above output shows the “cosine similarity” calculation using the “1-spatial.distance.cosine()” method.
Conclusion
To calculate the cosine similarity, the “Numpy” module functions, the “scipy” module function, and the “scikit-learn” module function are used in Python. The “Numpy” module provides functions such as “np.dot()” and “norm()” to calculate the dot and norm of the vector and then perform some calculations to calculate the cosine similarity. The “spatial.distance.cosine()” function of the “scipy” module is also used to calculate the cosine similarity. This Python guide presented a thorough guide on how to get the cosine similarity.
