A two-dimensional array having an equal size for each element is defined as a “Matrix”. In Python, matrices are represented as a Numpy array or using nested lists. The original matrix’s reciprocal is defined as a matrix’s inverse. When you multiply the inverse matrix by the original matrix, the identity matrix is returned in Python. Various methods are used in Python to compute the inverse of the input matrix.
This blog will explain the following methods to find the inverse of a matrix using numerous examples:
Method 1: Using Numpy Module
The “Numpy” module provides different functions to find the inverse of the matrix in Python. In the below examples, the “numpy.linalg.inv()” function and “numpy.matrix” class is utilized to find the inverse of the given matrix.
Note: If the determinant of an input matrix is “zero”, then it is singular and does not have an inverse. So, ensure that a given matrix is non-singular, i.e., the given matrix determinant must be “non-zero”.
Example 1: Using numpy.linalg.inv() Function
The “numpy.linalg.inv()” function is used in the below code to compute the inverse of the matrix:
Code:
import numpy
val = numpy.array([[2,12],[18,15]])
output = numpy.linalg.inv(val)
print(output)
In the above code, the “numpy.array()” function is used to create the array matrix. The “numpy.linalg.inv()” function accepts the variable “val” as an argument and returns the inverse of a given matrix.
Output:
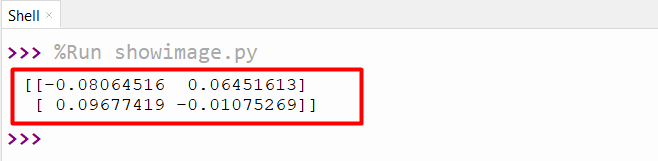
The inverse of the input matrix has been successfully calculated using the “numpy.linalg.inv()” function.
Example 2: Using numpy.matrix Class
The “numpy.matrix” class has an attribute “numpy.matrix.I” that calculates the inverse of the input matrix. Here is an example of how we can do that in Python:
Code:
import numpy
output = numpy.matrix([[2,12],[18,15]])
print(output.I)
In the above code, the “numpy.matrix()” is used to initialize a two-dimensional array matrix. The “numpy.matrix.I” calculates the inverse multiplication of a given matrix.
Output:
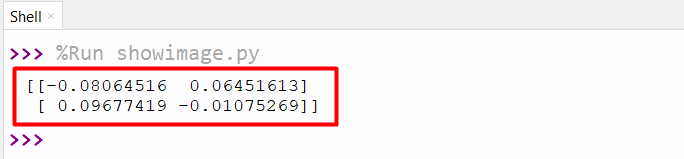
The inverse matrix of the given number has been successfully calculated using the “numpy.matrix” class.
Method 2: Using scipy.linalg.inv() Function
To calculate scientific and technical computing the “scipy” library is used in Python. The “scipy.linalg.inv()” function is the fastest way to calculate the inverse of a matrix. In the example given below, the “scipy.linalg.inv()” function of the “scipy” module is used on the numpy matrix:
Code:
import numpy
from scipy import linalg
output = numpy.matrix([[5,2],[3,4]])
print(linalg.inv(output))
In the above code, the “numpy.matrix()” creates the square matrix in a program. The “linalg.inv()” accepts the square matrix as an argument and returns the inverse of the matrix.
Output:
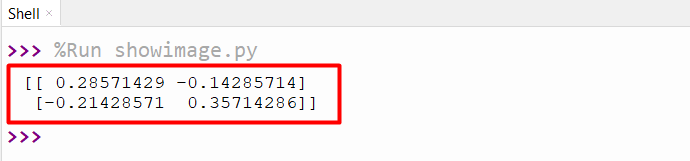
The above output shows the inverse matrix.
Conclusion
To get the inverse of the matrix, the “numpy.linalg.inv()” function, “numpy.matrix” class, and the “scipy.linalg.inv()” function is used in Python. The “numpy.linalg.inv()” is used to get the inverse of the square matrix. Similarly, the “scipy.linalg.inv()” function is used in Python for large matrix calculation. This post presented a detailed guide on computing the inverse of a matrix in Python.
